Puzzle Piece 7: The Photoelectric effect

Any discussion on any wave model is usually interrupted quickly by a “… but the photoelectric effect proves that light is quantized!”, and any further discussion is often impossible because of that. So it seems worthwile to have a separate page on just this topic alone.

Photoelectric Effect - Chemistry Steps
https://general.chemistrysteps.com/photoelectric-effect/

First I will briefly outline the concept of resonance, and summarize the main thought in the context of the photoelectric effect, then give a summaries of several related papers.

Resonance Example 1: Microwave

If you have ever used a microwave oven, then you have used a resonance effect involving electromagnetic waves.

https://www.electricalelibrary.com/en/2018/05/03/how-a-micro-wave-oven-works/

Microwave ovens operate using microwaves, a type of electromagnetic wave, which have a specific frequency. In microwave ovens, this frequency is typically around 2.45 gigahertz (GHz).

The principle of resonance comes into play because this frequency is close to the resonant frequency of water molecules. A resonant frequency is a natural frequency at which an object or substance, such as a water molecule, oscillates with the least amount of external force. When an object is subjected to an oscillating force that matches its resonant frequency, it will start to vibrate with a greater amplitude. This is known as resonance.

When the microwaves pass through food in the microwave oven, they make the water molecules in the food vibrate by matching their resonant frequency. This vibration causes friction between the molecules, and this friction generates heat. This heat is what cooks the food in the microwave oven:

Water molecules are polar, which means they have a positive end and a negative end. The oxygen atom carries a slight negative charge, while the two hydrogen atoms carry a slight positive charge. This gives water its dipole property.

https://www.ozmo.io/cooking-with-microwaves-how-water-molecules-are-excited-to-produce-heat/

Due to the polar nature of water molecules, they attempt to align themselves with the changing electric field because opposite charges attract each other. Since the electric field oscillates, it changes direction rapidly, billions of times per second. As a result, the water molecules also rotate or try to rotate billions of times per second to keep aligning themselves with the field.

This rapid rotation causes the water molecules to collide and interact with other molecules, causing them to move faster. In a substance, the speed of molecular movement is directly related to its temperature. Thus, the more the water molecules move (due to the microwave-induced rotations), the hotter the substance gets. This is how microwaves heat food.

Resonance Example 2: Guitar Strings (and Tuning Forks)

There are of course many examples of resonance involving sound waves, including singers that can shatter glass or a tuning fork that makes another tuning fork vibrate. Let’s look at one example with two guitars in more detail:

When you pluck a string on a guitar, it begins to vibrate at its fundamental frequency, along with several overtones or harmonics, which are multiples of this fundamental frequency. These vibrations cause the surrounding air molecules to vibrate at the same frequencies, producing sound waves.

If there’s another guitar nearby, these sound waves will reach it and interact with its strings. Each string of this second guitar has its own set of natural frequencies at which it prefers to vibrate, which are determined by factors such as its length, tension, and mass.

Tuning Fork example: https://ecampus.matc.edu/mihalj/scitech/unit6/sound/sound.htm

If the frequency of the sound waves produced by the first guitar matches the natural frequency of a string on the second guitar, that string will start to vibrate in response. This is due to resonance: when a system is subjected to an oscillating force (in this case, the pressure variations of the sound wave) that matches its natural frequency, it will start to vibrate with a larger amplitude. This is why you’ll see and hear the string on the second guitar vibrating, even though you didn’t pluck it.

This resonant interaction between musical instruments is the same principle that can cause a wine glass to shatter when a singer hits exactly the right note: the resonant frequency of the glass. It’s all about matching the frequency of an external force or wave to the natural frequency of another system.

Resonance Example 3: MRI

Magnetic Resonance Imaging (MRI) is a medical imaging technique used to visualize detailed internal structures of the body. It uses a strong magnetic field and radio waves to affect the hydrogen atoms in the body.

In an MRI machine, a strong magnetic field is used to align the spins of the hydrogen atoms in your body. Under normal conditions, the spins of these hydrogen atoms are randomly oriented. However, when placed in a magnetic field, they align with the direction of the field.

Once the spins are aligned, a pulse of radio waves at a specific frequency known as the Larmor frequency is applied. This radio frequency is in resonance with the spin precession frequency of the hydrogen atoms (precession is a change in the orientation of the rotational axis of a rotating body).

Diagram of magnetic fields' effect on proton alignment
https://www.khanacademy.org/test-prep/mcat/physical-processes/proton-nuclear-magnetic-resonance/a/magnetic-resonance-imaging-mri

The radio waves “flip” the spins of the atoms. After the pulse is turned off, the hydrogen atoms return to their original spin state in alignment with the magnetic field. As they do so, they emit radio waves of their own.

These emitted radio waves are detected and used to construct an image. The rate at which the atoms return to their original state varies depending on the type of tissue and its environment, which allows for the differentiation between different types of tissue in the image.

In the case of Magnetic Resonance Imaging (MRI), both the frequency and intensity of the radio waves have important roles:

Frequency:

  • The frequency of the radio wave pulse is set to match the precession frequency (also known as the Larmor frequency) of the hydrogen atoms in the magnetic field. This is the frequency at which the spins of the hydrogen atoms wobble, or precess, around their alignment with the magnetic field.
  • If the radio frequency is off, it will not effectively flip the spins of the hydrogen atoms, and the signal that is detected will be weak or nonexistent. This is because the energy of the radio wave needs to match the energy difference between the two spin states of the hydrogen atoms, and this energy difference depends on the strength of the magnetic field and the gyromagnetic ratio (a property of each type of atom).
  • The specific frequency needed can be adjusted by altering the strength of the magnetic field, which is why MRI machines often have adjustable magnetic fields.

Intensity:

  • The intensity of the radio wave pulse corresponds to intensity per unit time and area.
  • Increasing the intensity increases the number of chances the wave has to interact with hydrogen, and thus the number of hydrogen atoms that can be flipped at a given time. This can lead to a stronger signal and faster imaging times.

In summary, the frequency of the radio wave pulse needs to be precisely controlled to match the Larmor frequency of the hydrogen atoms, and the intensity of the pulse determines the strength of the signal that is received and thus the speed and quality of the imaging.

Other examples of resonance

  • LC Circuits: In electronics, an LC circuit (consisting of an inductor and a capacitor) can store electrical energy oscillating at a frequency determined by the values of L (inductance) and C (capacitance). When driven at that frequency, the circuit exhibits electrical resonance, resulting in a large oscillating current or voltage.
  • Radio Tuning: When you tune a radio, you’re adjusting the frequency of an internal LC circuit to resonate with the frequency of the desired radio station. This resonance amplifies the signal of that station over others.
A simple crystal radio can receive AM radio signals and convert them to sound.
https://electricalacademia.com/electronics/radio-transmitter-and-receiver-working-block-diagram/
  • Atomic Clocks: In atomic clocks, the resonance between the microwave frequency and the energy level transition frequency of atoms (usually cesium or rubidium) is used to keep extremely precise time.

If the frequency is too low…

In all these example, it was quite obvious that the frequency of the oscillations matter. So, what happens if the frequency is too low but the intensity is high?

Microwave oven:

If the frequency is too low, the energy will not be sufficient to trigger this rotation effect. The molecules will not absorb the wave energy effectively, and thus won’t experience an increase in kinetic energy or heat up.

If you increase the intensity of a wave with a frequency too low to interact effectively with water molecules, you’ll just have more of a wave that the water isn’t absorbing. The result is that the water doesn’t heat up, no matter how strong the intensity is.

Guitar Strings:

Similarly for guitars, a string will only vibrate significantly if the frequency of the incoming sound wave matches the natural frequency of the string. This is the principle of resonance.

The intensity of the plucking (how hard you pluck the string) does affect the amplitude (loudness) of the sound wave produced, but it does not change the frequency of the sound wave. So, even if you pluck the string on the first guitar very hard, a string on the second guitar will only vibrate if the frequency of the sound wave matches its natural frequency.

In other words, plucking a guitar string harder (increasing the intensity) will make the sound louder, but it won’t cause more strings to resonate. If the frequencies don’t match, there’s no significant resonance, no matter how hard you pluck the string.

If we increase the intensity….

So what do we expect to happen if we increase the intensity of the wave?

Microwave:

if you increase the intensity of the microwave (i.e., increase the number of microwave photons), you’re increasing the number of chances for microwave photons to interact with water molecules and cause them to rotate. As a result, more water molecules respond by rotating and this increased friction between molecules leads to heating of the water.

However, the energy of each individual microwave photon (and thus its ability to make a water molecule rotate) depends on its frequency, not its intensity. So while a higher intensity microwave will interact with more water molecules at once, the frequency of the microwave still needs to be correct for the rotation of the water molecules to happen effectively.

Guitar:

The intensity of the plucking (how hard you pluck the string) affects the amplitude of the sound wave you create, and thus the loudness of the sound. If you pluck the string harder, you’ll create a louder sound wave (one with larger compressions and rarefactions). This louder sound wave will only affect guitars where the frequency matches.

The loudness means it can affect guitars further away, and if you had a room full of guitars, more guitars with a matching frequency would start to make a sound.

Summary of resonance so far

Microwave:

  • Frequency:
    • The frequency of the microwaves determines whether the water molecules in the food will resonate and rotate.
    • The microwave frequency should match the natural frequency at which water molecules rotate. If it doesn’t, the microwaves won’t effectively heat the food.
  • Intensity:
    • The intensity of the microwaves corresponds to amplituded of the EM wave
    • Increasing the intensity (i.e., power level) of the microwave increases the chance that a water molecule will respond, and thus the number of water molecules that can be made to rotate at a given time.
    • However, it doesn’t change the rotation frequency of the molecules

Guitars in a room:

  • Frequency:
    • The frequency of the sound wave produced by a plucked string determines which strings on other guitars will resonate.
    • Only the strings that are tuned to the same note as the plucked string (or a harmonic of that note) will resonate significantly.
  • Intensity:
    • The intensity of the sound wave corresponds to the amplitude of the wave, or how hard the string is plucked.
    • Increasing the intensity of the plucking makes a louder sound, which carries more energy to the other guitars.
    • This can cause resonating strings on other guitars to vibrate more intensely, but it won’t cause other strings to start vibrating if their frequencies don’t match that of the plucked string.
    • Higher intensity (louder sound) can allow guitars further away to respond, as the sound wave can reach further without dissipating below the threshold of audibility or resonance.

Resonance in the photoelectric effect?

So how could resonance play a role in the photoelectric effect?

Electrons in a metal occupy energy levels in what’s known as a “band structure”. In simple terms, the energy levels that electrons can occupy in a metal are not isolated, but form continuous bands.

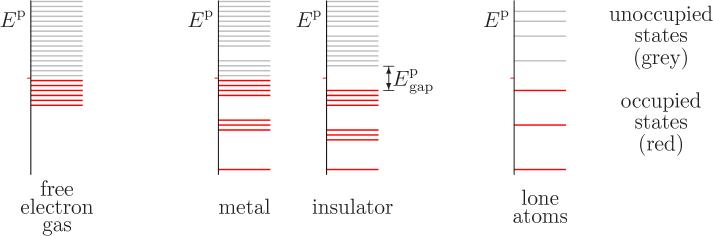
\begin{figure}\centering {}% \setlength{\unitlength}{1pt} \begin{picture}(4... ...ox(0,0){states}} \put(175,50){\makebox(0,0){(red)}} \end{picture} \end{figure}

The highest energy band that electrons typically occupy at absolute zero temperature is known as the Fermi level. Around the Fermi level, there are many closely spaced energy levels that electrons can occupy.

When light (or any electromagnetic radiation) with frequency corresponding to the energy difference between these levels interacts with the metal, the electrons can absorb the energy and get excited to higher levels. If the absorbed energy is enough to overcome the work function of the metal (the energy required to remove an electron entirely), the electron can be emitted from the metal, a process known as the photoelectric effect.

Simlar to the examples of the microwave example and MRI, if the frequency of the EM wave is too low, it will not resonate with the electrons and will have no effect, no matter how large the intensity is.

Once the energy delivered to an electron exceeds the work function of the metal, the electron will be freed. Higher frequency waves would free electrons that are at a higher band level. Due to energy conservation, when the wave interacts with an electron, it transfers its energy to the electron as kinetic energy.

The energy of the incident wave is not lost but transferred: first to overcome the work function (binding energy) and the surplus to the kinetic energy of the ejected electron. Therefore, higher frequency (higher energy) waves result in electrons being ejected with higher kinetic energy.

This explains why increasing the frequency (while keeping it above the threshold) leads to faster ejected electrons.

In an electromagnetic wave, increasing the intensity of the light wave would correspond to increasing its amplitude. This would not change the frequency of the wave, but would instead increase the strength of the oscillating electromagnetic fields that make up the wave.

Increasing the intensity (amplitude) of the light would increase the rate at which electrons are ejected, assuming the light’s frequency is at or above the threshold frequency.

In short:

  • Frequency:
    • The frequency of the incoming light wave determines the energy of the wave.
    • Only if the frequency of the light wave is above a certain threshold frequency (corresponding to the work function of the metal), will the light wave have enough energy to remove an electron from the metal.
    • If the frequency of the light wave is increased beyond this threshold, the energy from the light wave is transferred to the ejected electron as kinetic energy. This results in photoelectrons (ejected electrons) moving faster.
  • Intensity:
    • The intensity of the light wave corresponds to the amplitude of the wave, or roughly speaking, how many waves are hitting the metal per unit time.
    • Increasing the intensity of the light wave increases the number of waves hitting the metal and thus, increases the number of chances for light waves to interact with electrons.
    • However, it doesn’t change the minimum frequency required to remove an electron, or the frequency-dependent energy that the light wave carries. So, even with a high-intensity wave, if the frequency of the light is below the threshold, no electrons will be ejected.

Summaries of a few relevant papers

Below is a summary of several papers that explain the photoelectric effect without the need of photons:

Summary of “The Photoelectric Effect Without Photons”

The photoelectric Effect without Photons, Willis E. Lamb
https://ntrs.nasa.gov/citations/19680009569
Direkt link to pdf

This paper is presenting a discussion on the photoelectric effect from a perspective that does not require the concept of “light quanta” or photons. The authors explain that it is possible to understand the photoelectric effect solely in terms of a classical electromagnetic field interacting with quantized atomic matter.

Here are the key points from the paper:

  1. A classical electromagnetic field bathes atoms, each of which has one electron. The atoms have a ground state and a quasi-continuum of excited states.
  2. When the field interacts with the electron, the electron can transition from the ground state to any of the excited states. The probability of an electron being raised to a certain excited state is appreciable only if the energy associated with that state matches the energy of the electromagnetic field (expressed in terms of frequency).
  3. This leads to the derivation of the Einstein photoelectric equation, hν = Φ + E, where hν is the energy of the incoming electromagnetic wave (classically considered), Φ is the work function (minimum energy required to remove an electron), and E is the kinetic energy of the ejected electron. Notably, this derivation does not require the photon concept.
  4. The paper also explains that the total probability of finding a photoelectron is directly proportional to the light intensity, consistent with experimental observations of the photoelectric effect.
  5. Finally, the authors argue that their approach, even though it doesn’t consider the “photon” concept, does not imply a time delay in the photoelectric effect. The transition of the electron starts as soon as the electromagnetic field is turned on.

In summary, this paper offers an interpretation of the photoelectric effect where the electromagnetic field is treated classically, and only the matter (atomic electrons) is treated quantum mechanically. The photon concept, while widely accepted and used, is not invoked in this interpretation.

The Anti-Photon

Anti-photon (W.E.Lamb, Jr.)

This paper discusses the nature and behavior of radiation and light through the lens of quantum mechanics. Here is a summary:

  1. The paper critiques the popular interpretation of radiation as particles or “photons,” and suggests we must instead see light and radiation as wave phenomena described by Maxwell’s equations. In this view, the idea of a “photon” can be misleading and should be abandoned.
  2. It discusses different types of optical and quantum mechanical systems, including closed optical resonators, mirrors, refraction and reflection at interfaces of different refractive indices, beam-splitting problems, total internal reflection, Young’s two-slit diffraction arrangement, Fabry-Perot plates, and multi-port devices like a Michelson interferometer.
  3. It presents radiation as dynamically equivalent to a system of quantum-mechanical simple harmonic oscillators. This leads to the exploration of different states of such a system, including eigenstates of energy, coherent superpositions of eigenstates, and mixtures described by a density matrix.
  4. It discusses the implications of viewing the radiation field as composed of several modes, which are dynamically equivalent to simple harmonic oscillators. Depending on the complexity of the system (number of modes), the paper states that the concept of “photons” can become increasingly difficult and potentially inappropriate to apply.
  5. In more complex scenarios, like when an atom in an unbounded region undergoes spontaneous transitions, an infinite number of modes may be required to describe the system. In such cases, using a quantum mechanical description of the system will yield more meaningful results.
  6. Finally, the paper argues against the wave-particle duality, seeing it as a misleading concept born out of a lack of understanding of quantum mechanics. It emphasizes that light and radiation do not consist of particles, but are better described by fields, not unlike the fields described in classical electrodynamics.

The overall message of the paper is to urge a rethinking of the traditional “photon” concept, pushing for a stronger reliance on wave phenomena and quantum mechanics to describe radiation.

The concept of the photon

The idea of the photon has stirred the imaginations of physicists ever since 1905 when Einstein originally proposed the use of light quanta to explain the photoelectric effect. This concept is formalized in the quantum theory of radiation, which has had unfailing success in explaining the interaction of electromagnetic radiation with matter, seemingly limited only by the ability of physicists to perform the indicated calculations. Nevertheless, it has its conceptual problems—various infinities and frequent misinterpretations. Consequently an increasing number of workers are asking, “to what extent is the quantized field really necessary and useful?” In fact the experimental results of the photoelectric effect were explained by G. Wentzel in 1927 without the quantum theory of radiation. Similarly most electro‐optic phenomena such as stimulated emission, reaction of the emitted field on the emitting atom, resonance fluorescence, and so on, do not require the quantization of the field for their explanation. As we will see, these processes can all be quantitatively explained and physically understood in terms of the semiclassical theory of the matter–field interaction in which the electric field is treated classically while the atoms obey the laws of quantum mechanics. The quantized field is fundamentally required for accurate descriptions of certain processes involving fluctuations in the electromagnetic field: for example, spontaneous emission, the Lamb shift, the anomalous magnetic moment of the electron, and certain aspects of blackbody radiation. (The Compton effect also fits here, but see later under references 8b and c.) Here we will outline how the photon concept originated and developed, where it is not required and is often misused, and finally where it plays an essential role in the understanding of physical phenomena. In our discussion we will attempt to give a logically consistent definition of the word “photon”—a statement far more necessary than one might think, for so many contradictory uses exist of this elusive beast. In particular consider the original coining of the word by G. N. Lewis:

“[because it appears to spend] only a minute fraction of its existence as a carrier of radiant energy, while the rest of the time it remains an important structural element within the atom…, I therefore take the liberty of proposing for this hypothetical new atom which is not light but plays an essential part in every process of radiation, the name photon!”

Clearly the present usage of the word is very different.

Summary of Nature of Photoelectric Effect in a Ge-on-Si SPAD at Ultralow Energy in Incident Pulsed Laser Radiation

Nature of Photoelectric Effect in a Ge-on-Si SPAD at Ultralow Energy in Incident Pulsed Laser Radiation
Direct link to pdf

This paper proposes a novel approach to explaining the interaction of light (particularly near-infrared radiation) with a material, in this case, germanium and silicon in a Single-Photon Avalanche Diode (SPAD), using wave concepts. It explores how electromagnetic waves, when interacting with electrons in these materials, can lead to a constructive interference phenomenon that intensifies radiation at a specific point within the lattice. This approach supports the wave model of light because it leans heavily on wave concepts such as interference, resonance, and re-emission of energy due to wave interaction with electrons and atomic dipoles.

Two types of secondary emission by electrons are considered:

  1. Due to accelerated movement of an electron: In this scenario, all electrons within a material can potentially re-emit energy due to their movement induced by the electric field of incident radiation.
  2. Resulting from an oscillating dipole: This form of emission is conceptualized with the atom considered as a set of dipole oscillators, and is contributed by the electrons occupying higher energy orbits around the atomic nucleus. However, the contribution of such dipole-kind emission is limited to electrons occupying lower energy orbits as they interact more significantly with Near Infrared (NIR) optical radiation.

The paper uses mathematical modeling to estimate the resultant electromagnetic fields at a certain point C, which may be induced by the coherent summation of the fields re-emitted by all electrons in Ge and Si layers within a device called a Single-Photon Avalanche Diode (SPAD).

It was observed that, while the enhancement of the resultant field due to the electron re-emission fell short of the desired magnitude, the re-emission by dipoles could theoretically achieve a significant enhancement factor, given the condition that the frequency of the incident radiation equals the resonant frequency of the oscillator.

The authors also mention an interesting phenomenon associated with heavily doped semiconductors, such as p-Ge used in SPADs, where local fluctuations of the internal electric field in the material could effectively narrow the bandgap. This peculiarity might offer a resolution to the energy conservation issue associated with the dipole re-emission scenario.

References