Previous puzzle: Puzzle Piece 3: What’s special about Special Relativity?
Normally when we talk about light, we mean visible light. But, all electromagnetic waves, including infra red, X-Rays and even radio waves are the same type of wave, and could be considered “light” as well.
Everyone seems to know that light is quantized (called Photons) and can behave either like a wave or a particle. Today in QM the assumption is that light is inherently quantized and can be viewed as both a wave and a particle. But what does that really mean, and is it really true that photons can be explained using point like particles, or can they still be explained using classical waves?
Black body spectrum
The origin of the light quantization is the black body spectrum, which Planck could not explain with classical physics. So he introduced the Planck constant h in order to make this work. At that time, they did not yet have the Schrödinger equations nor did they consider relativistic effects either. Today, it looks like it is possible to explain the black body spectrum with classical waves, when considering the new insights, as is described here.
Photoelectric Effect
Another puzzle was the photoelectric effect, where light causes electrons to be emitted in a metal.
The interesting part is that below a certain frequency, no matter how intense the light is, no electrons are emitted, so the question was why. Einstein was explained this effect using quantized “photons”, which he considered to be point like.
It looks like in the meantime, it is also possible to explain this effect another way. The second approach involves a resonance effect, where the frequency of the light has to match the frequency of electrons in the metal to be able to affect them.
There are papers such as this one that show how the photoelectric effect could be explained with classical waves, which do not require point like particles.
Radio
Let’s think about radio waves. It is clear that when light is emitted due to electrons in an atom that change energy levels, that this light is quantized, because it was emitted that way. But what about radio waves? If they were quantized, their energy would be extremely small and hardly detectable.
The signal that is generated in radio waves is created using electrons that are not bound to atoms, using electric circuits. So there seems to be no inherent logical reason for the wave to be quantized. We all know that radios work, and in fact, there are even radio that require no power at all. These are called crystal radios. The question for me is then, are radio waves also quantized? The second question is: if light is always quantized, is there really a need to consider photons to be “point like” particles, or can they be explained using classical waves. To me it seems at least the second question can be answered, as all effects so far have a reasonable explanation using classical waves.
Einstein wrote in 1951 to his friend Michele Besso: “All these fifty years of conscious brooding have brought me no nearer to the answer to the question, ‘What are light quanta?’ Nowadays every Tom, Dick and Harry thinks he knows it, but he is mistaken”.
The (other) Heisenberg
Let’s talk about Heisenberg for a moment – not Walter White, the real Heisenberg, who came up with the uncertainty principle. The fact that for any particle, one cannot measure location and momentum exactly at the same time.
If we look at this in the context of waves, as in sound waves, then maybe it does not sound so strange. Basically, the principle says that the error in the position (dx) times error in momentum (dp) is larger or equal to ħ/2:
where ħ is the reduced Planck constant.
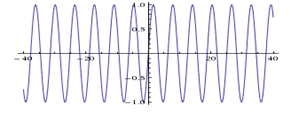
So what does that mean in the context of sound? A pure sine tone (say 440 Hz) has an exact frequency, but has no clearly defined starting and ending position:
Imagine you play this tone on an instrument, say a violin. Then you hear just that one frequency, and there is no beginning or end of that tone (except when the player begins and ends of course). So that sine wave extends in space for as long as the player plays that tone. It is not localized – it makes no sense to talk about location, as it is the same for the entire duration of the sound.
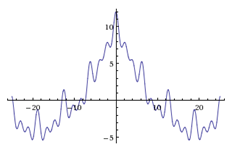
Now what does an exploding balloon sound like? It’s the opposite of a pure sine wave: a popping balloon has quite a specific location, but the frequency of that sound is not one pure tone, but a mixture of many frequencies. How can this be represented? Basically by adding a bunch of sine waves (Fourier) together, to get the shape of the explosion sound: below I added a bunch of cos curves – the more you add, the more localized the sound gets, but the more frequencies are mixed in, so the harder it gets to determine a frequency.
You can either measure the frequency, but then you can’t tell quite exactly where the sound begins or ends, or else, you measure the location, but then you can’t quite tell what frequency the tone had. In fact, the perfect impulse has an infinite number of frequencies, and it doesn’t even make sense to talk about measuring the frequency in that case, because there is no clearly defined frequency. In the other case, it makes no sense to say where exactly the tone is, because it has no clear beginning or end.
This is true for any kind of wave, whether we talk about sound waves, water waves, light waves or matter waves. If matter is composed of true waves, then maybe the idea that for a “particle” you can either determine it’s location or it’s momentum, but not both at the same time, does not seem so strange anymore – it is simply a natural consequence of any wave.
Next puzzle: Puzzle Piece 5: The Doppler Challenge
Summary Table
Space-density Universe
|
Space-Time Universe
|
|
| Tags | elastic solid, crystal universe, optical-mechanical analogue, space exists | Minkowski, space-time, absolute space does not exist |
| GR Metric Tensor | space-density (space with compression) | space-time |
| Cause of Gravity | refraction (density gradient, optical) | curvature of space-time |
| Photon | quantized wave, similar to phonon quasiparticles in crystal (vibrational mode), there are no photon “particles” | probability density wave function, no “real” wave, probability of finding photon |
| Double Slit Experiment | real waves interfering (like phonons) | parallel universes, no real wave, “consciousness” ,probabilistic… |
| Schrödinger Wave Equation | describes real waves, rotational waves in an elastic solid. There are no particles | probability of finding a particle, there are no real waves |
| What is space? | An elastic solid (not made of matter). Matter and light moves though space as waves move through a crystal | There is no absolute space |
| Special Relativity | Time dilation and length contraction are consequence of any wave system. Any wave has a maximum speed in any given medium. | There is no intuitive explanation. It follows from the constancy of the speed of light for each observer |
| Speed of light | c, constant in absolute space. Also c for each observer, due to time dilation | c is constant for each observer. There is no absolute space |
| Twin Paradox | No paradox. Whoever moved slower relative to absolute space ages faster. | If A is considered to be at rest, B ages more slowly, and vice versa. There is no clear answer as to who ages faster (if cleverly engineered –see post on that) |
| Uncertainty Principle | Natural consequence of any wave system | Due to wave property of matter and light (but only probabilistic) |
Links
Photons
- Photons and the Quantum Enigma
- On the single photon nature
- Quantized fields of single photons
- https://www.intechopen.com/online-first/quantized-field-of-single-photons
- Blog about Photons
- Wave function collapse
- Radio wave are not necessarily quantized: https://www.researchgate.net/publication/327578880_Man-Made_Electromagnetic_Radiation_Is_Not_Quantized
- Photoelectric effect without photons:
Black Body Spectrum
- Black body spectrum without quantum assumptions
- Black body spectrum in classical physics
- Classical explanation
Uncertainty Principle
- Wikipedia: http://en.wikipedia.org/wiki/Uncertainty_principle
- The Uncertainty Principle: http://www.mtnmath.com/whatrh/node72.html
- The Open University: http://www.met.reading.ac.uk/pplato2/h-flap/phys10_2.html (chapter 4)