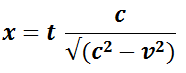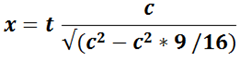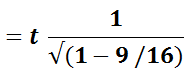Previous puzzle: Puzzle Piece 2: What’s the Matter with Matter?
1. Time Dilation
You probably think that special relativity is hard to understand and explain (I mean, so that your grandmother would understand it), and that his surely has nothing to do with any of that “Crystal Universe” idea or “The Classical Wave Theory of Matter”.
So let me give it a shot: all you need to know is 2 things – and even that is overkill. You need no math to understand this at all, only if you want to see that the result is the same as Einsteins result, and only if you actually want to calculate things:
- the Pythagorean formula
. - that waves in a medium have a particular speed c
(such as sound in air (w/o wind), sonar in water, earthquake waves, phonons in a crystal, water waves etc)
First, the easiest example – one that you can actually try yourself in real life:
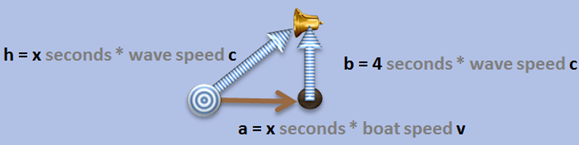
Take a regular boat, put it on a still lake. At the end, we build a “water wave clock”: we add a wooden frame with a stick at the end. We “start” the clock by making waves with a stick. The clock “ticks”(rings) when the wave front reaches the bell:
Note that the wave extends in all directions. For simplicity, we will use arrows – even though of course the waves don’t go just in one direction. But it shows the direction from the start of where the wave originated to the end, where the “bell” rings. When the boat is stationary, this is what it looks like:
(I know I am going kind of slow here, but I really want my grandmother also to understand this :-).
What does it look like when the boat is moving?
You can see that the distance the water wave has to travel is now longer, because the boat is moving away. Say it took 4 seconds when the boat was still for the ring to bell. How long do you think it takes now? It clearly takes longer now – but how long depends on how fast the boat is moving. How can we compute that?
Note: You can skip all the math part below if you like, and instead jump right to “Length contraction”. If you understood the logic so far, that is all you really need to understand “time dilation”. It is literally not more complicated than that! Yes, of course, the “strange” part to wrap you brain around is to think about why this should apply not just to water waves but to us (more on that below, but it applies to all waves, including matter “waves” such as electrons and protons…).
(Note: in water, the speed of the wave is depending on the wave length… to make this work with water, we have to use the same wave length, such as 10cm from water crest to water crest)
All we need to know is that distance = time * speed, and the Pythagorean formula:
The distance h (the hypothenuse) is the number of seconds x we want to compute * the speed c of the water wave. We know that when the boat was still, it took 4 seconds for the wave to reach the bell. The distance b = 4 seconds * wave speed c (I know, of course we could simply measure it, but the point is that we want to get a formula to compute these things ;-). The distance a is how far the boat went, so a = the speed v of the boat, times the number of (unknown) seconds x we want to compute.
All we do now is apply the Pythagorean formula, and solve for x! One small change: instead of putting 4 for the 4 seconds, let’s use t.
(x*v)2 + (t*c)2 = (x*c) 2
x2 * c2 – x2 *c2 = t2*c2
x2 (c2 – v2) = t2 * c2
x2 = t2 * c2 / (c2 – v2)
Example with real numbers: say in the stationary case it took t = 4 seconds. Let’s pick a speed v for the boat, such as 3/4 as fast as the wave speed c (for a wave with 10cm wave length in clean water, it travels about 30cm/second): v = c*3/4.
We replace v with c*3/4 in the formula and get:
, 
x = 1.5 * t = 1.5 * 4 seconds = 6 seconds
What happens if the boat is going as fast as the wave speed c? Then the clock never ticks! Because the wave front can never reach the bell…
This is where this particular analogy ends of course, and as we said, for surface water waves, the wave speed depends on the frequency, and also because the boat is not a wave…
Following is a more analogous example of the “crystal universe” – it is really exactly the same, except that we replace the water with the crystal (or elastic solid like Jell-O), and that we replace the water clock with a “phonon” clock (sound), and that we replace the boat with a “matter wave” boat:
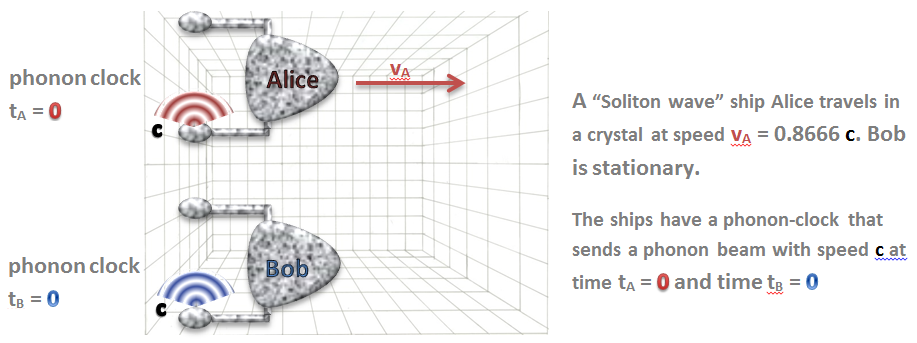
The two ships have a phonon clock attached. Each “tick” in the clock is when the phonon beam from the bottom part of the clock reaches the detector on the top. c is the speed of the waves (phonon waves) in that crystal.
Alice boat is moving at speed v = (0.866 * c) (to get an even result :-).
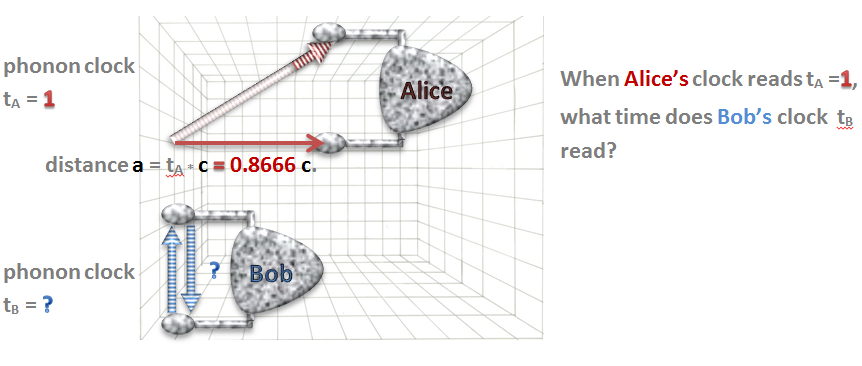
We do the same thing as we did with the regular boat. All we have to do is use the Pythagorean formula:
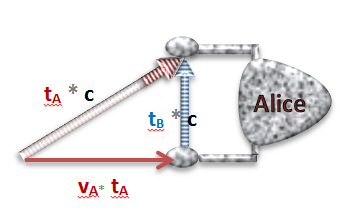
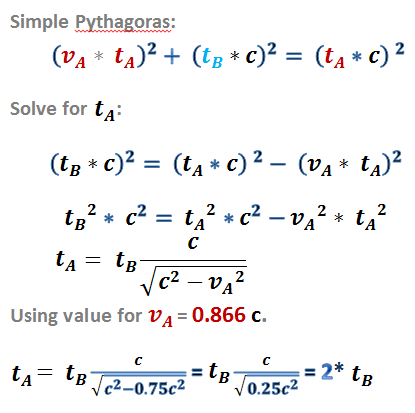
The answer for this example is: Bob’s “clock” runs twice as fast as Alice’s clock. In this example, because the ships themselves are composed of (soliton) waves, they can never go faster than c either!
For an animated version of this, please check out Robert Close underwater relativity!
How does this translate to “our” world? If photons are actual (quantized) waves like phonons, and if matter waves are also true waves (and not just probabilities for particles), waves in a “solid space”, then we get *exactly the same result*. In that model it is completely logical, that photons always travel at the wave speed c, and that no wave, so no matter wave either, can ever go faster than c.
The entire “time dilation” then in this model is simply a wave phenomenon. There is absolutely nothing magical about it! You get the same result for *any* wave system.
If you think about it, what are clocks? All our clocks are at end made of either light or matter. And if matter are waves, then of course, any moving clock would tick slower. So in this “crystal” model, it is not the case the that (abstract) time is really moving slower. It is simply the actual clocks that tick slower (because the paths of moving clocks are longer!). We could even argue, is there an abstract concept of time.
In the “mainstream” (space-time) version, this is a bit different. In that model, there is no absolute time, and there is no absolute space either. Clocks are not ticking slower, it is actual time that is slower for that particular “frame” (that particular object). And the speed of light in that model is not constant in an absolute sense, since in that model, there is no absolute space either. In the space-time interpretation, the speed of light is constant for each observer. This might seem like a detail, but it means you can no longer use “common sense” to explain it. And also, in that model, special relativity has nothing to do with waves.
You might say: but, it has been shown that light is in fact the same for any (moving) frame. Yes, that is true! And I will show next how indeed, for any moving or non-moving observer, the speed c always *appears* the same, even though it is actually constant in the absolute sense:
So let’s measure the wave speed c in two situations, when then boat is stationary, or when the boat is moving:
a) Stationary Situation
The distance b between the source of the wave clock and target bell is time * wave speed c. We want to know how kind of c that the person in the boat measures, with his clock. Hence we use his time tA. The distance b is known of course, the person in the boat can just measure the frame width. Therefore c = b/tA.. The time tA is 1, since this is how our clock works: when the ring bells, the time ticks once. Hence c = b
b) Moving Situation
When the boat is moving, viewed from a stationary observer, the wave has to travel further, and the clock of the moving boat is running slower.
What wave speed does the person in the moving boat measure? Well, for him, one tick is still – per definition – the time it takes for the wave to hit the bell. For the moving observer, the time tA is still 1 tick. The distance b has not changed (the width of the frame). And again, c is the same: c = b
We will look at a more complicated situation in the length contraction section, but basically every observer will always measure the same speed of c, no matter whether the observer is stationary or moving.
2. Length Contraction and Doppler Effect (part 1)
We’ll do a simplified example first. Imagine we are on a still lake, and dipping a stick into the water at regular intervals from a boat. You get this familiar wave pattern below:
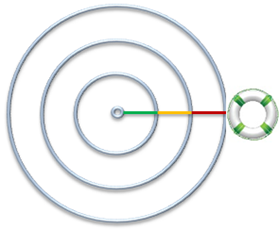
Notice how the distance between the wave crests is constant, and the same on both sides. Let’s use the number of wave crests 
as our measuring stick. We use it to measure the distance to say a life buoy:
The distance is 3 weave crests.
If we do the same thing in a uniformly moving boat, say at 2/3 of the speed of the wave in a horizontal direction, then it looks like this:
The distance between the weave crests is now 1/3 as it was before on the right (but still equidistant). So our measuring “stick” has shrunk to a third 
. Of course we notice that, because we are (in this examples) outside observers and can see that. If we were composed of the same kind of waves as in this example however, we would also have shrunk to 1/3 in the horizontal direction, and would not notice (a more detailed example on that later make this point clear).
This also illustrates the Doppler effect: The wave length has shrunk, and so if someone were listening (in a sound example) as the object approaches, then the frequency would be higher as in the stationary case:
If the boat is uniformly accelerating to the right, then the wave crests are no longer equidistant, they get shorter as we measure them towards the center:
So to a listener, the frequency would get higher and higher, and our measuring “stick” would get shorter and shorter…
For a much more detailed example, please take at the (animated) unterwater relativty by Robert Close:
http://www.classicalmatter.org/UnderwaterRelativity/ParallelLength.swf
And for a more “correct” version of this, with boats that are also made out of waves, see this animated example:
http://www.classicalmatter.org/UnderwaterRelativity/MatterWaves.swf
Next puzzle: Puzzle Piece 4: The (other) Heisenberg
Summary Table
Space-density Universe
|
Space-Time Universe
|
|
| Tags | elastic solid, crystal universe, optical-mechanical analogue, space exists | Minkowski, space-time, absolute space does not exist |
| GR Metric Tensor | space-density (space with compression) | space-time |
| Cause of Gravity | refraction (density gradient, optical) | curvature of space-time |
| Photon | quantized wave, similar to phonon quasiparticles in crystal (vibrational mode), there are no photon “particles” | probability density wave function, no “real” wave, probability of finding photon |
| Double Slit Experiment | real waves interfering (like phonons) | parallel universes, no real wave, “consciousness” ,probabilistic… |
| Schrödinger Wave Equation | describes real waves, rotational waves in an elastic solid. There are no particles | probability of finding a particle, there are no real waves |
| What is space? | An elastic solid (not made of matter). Matter and light moves though space as waves move through a crystal | There is no absolute space |
| Special Relativity | Time dilation and length contraction are consequence of any wave system. Any wave has a maximum speed in any given medium. | There is no intuitive explanation. It follows from the constancy of the speed of light for each observer |
| Speed of light | c, constant in absolute space. Also c for each observer, due to time dilation | c is constant for each observer. There is no absolute space |
| Twin Paradox | No paradox. Whoever moved slower relative to absolute space ages faster. | If A is considered to be at rest, B ages more slowly, and vice versa. There is no clear answer as to who ages faster. |
Links
Special Relativity:
- The Other Meaning of Special Relativity (Robert Close): http://www.classicalmatter.org/ClassicalTheory/OtherRelativity.pdf
- Classical Wave Theory of Matter (by Robert Close), chapter 2:
http://www.verumversa.com/ClassicalWaveTheoryOfMatter.pdf - Underwater Relativity: http://www.classicalmatter.org/UnderwaterRelativity.htm
Other:
- Hagen Kleinerts World Crystal:
http://users.physik.fu-berlin.de/~kleinert/papers/planckklcZN.pdf